BMI and Climbing Part 3, ALL 8a.nu Climbers
We’ve already written a few posts looking at BMI and climbing across a few different data sets, and now comes the final chapter!
We’ve combined every single ascent logged on 8a.nu with every profile to see if there’s a correlation between BMI and hardest grade climbed in the last 2 years. After filtering off climbers without a height or weight, we’re left with a grand total of 1,089 female climbers and 8,856 male climbers.
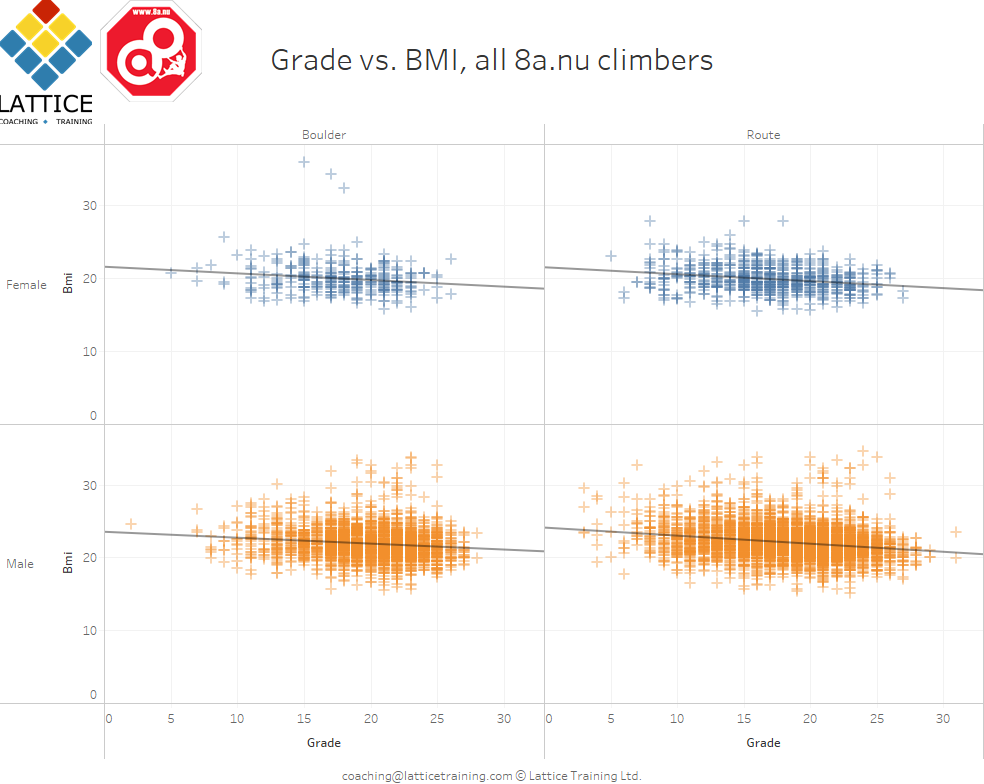
And the conclusion…is the same as in previous posts! From the data we have available at the moment there doesn’t seem to be a correlation between best grade climbed and BMI. Of course this doesn’t rule out the idea that short term weight, carefully controlled loss can be beneficial in the right circumstances, but it does suggest that long term, maintaining a low BMI is not correlated with achieving higher grades. In particular we note that the vast majority of climbers in the 8a.nu sample are in the ‘healthy’ 18.5 – 24.9 BMI range (1) regardless of max grade.
Note: The grade axis in the above graphs are a linear map from french sport grades and font boulder grades.







I think Tom Randall mentioned in an interview that there was a strong correlation between bodyweight and Grade. The correlation between Height and grade climbed he said was not observable purely because of the strong correlation of weight and height. So what do you learn from looking at the correlation between grade and weight divided by height squared? That seems like a very convoluted measure, and a correlation either somewhat hard to interpret or trivial because still dominated by the overwhelming correlation between weight and grade climbed.
Hey Stefan, while we have found weight is a better predictor than height in our multi-factor models I think BMI was still an interesting measure to look at (although it turns out to not be very helpful).
If we take a high level view, BMI attempts to measure how heavy an individual is for the height which would seem like a sensible thing to be concerned with when looking at climbers (until you get in to all the problems with BMI of course!) BMI uses weight / height^2 because height and weight are not linearly correlated (in theory the measure should be closer to weight / height^3 but in practice taller people are not perfectly scaled up versions of smaller people.)
Thanks Remus,
that makes a lot of sense. So if the BMI turns out not to be very helpful, just out of curiosity, have you attempted to find a better measure? I guess you have a lot of weight/height data at hand to see how the actual distribution looks like? You’d really expect it to be very important how heavy you are for your height, therefore maybe you just haven’t found the right measure for that yet?
Hey Stefan, the ideal measure (or at least a very interesting measure) would be body fat percentage as this would give you a good estimate for the muscle mass of the individual. However it’s historically proven very difficult to measure with any accuracy, especially if you need to do it in a cost + time efficient way i.e. where you dont have to go to a lab.
Could you give some details on the significance of the correlations for your linear models? It looks like the r-squared value would be pretty high for many of the regressions suggesting that there is a significant correlation between BMI and grade. The slope of the regressions is not steep indicating, as you say, that BMI doesn’t control grade climbed but this is not the same as saying BMI doesn’t correlate with grade climbed…
Agree with above comment by Iain, presenting both significance testing of the regression model and r-squared values as well as residuals is needed to be able to draw any valuable conclusions. Drawing conclusions based on the data presented above, without further statistical analysis is risky.
Interesting data anyhow,
Cheers!
Number of people with BMI over 30 !!??